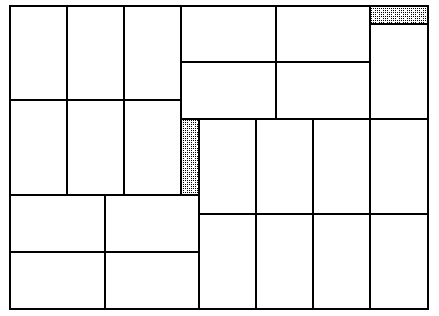
Figure 1. Optimal solution arrangement for instances (22, 16, 5, 3), (30, 22, 7, 4), (50, 36, 11, 7), and all instances within the same equivalence class.
Some PLP instances, with different dimensions, possess the same arrangement of boxes in an optimal solution. For example, the arrangement depicted in Figure 1 is an optimal solution to the instance (22, 16, 5, 3) where the shaded regions indicate unused (wasted) areas of the pallet. The same arrangement is also optimal to instances (30, 22, 7, 4) and (50, 36, 11, 7), among an infinite number of instances.
Figure 1. Optimal solution arrangement for instances (22, 16, 5, 3), (30, 22, 7, 4), (50, 36, 11, 7), and all instances within the same equivalence class.
If we draw a vertical or horizontal line across a loaded pallet, as in Figure 2, it crosses a number of boxes. If the dimension of a box crossed by the line is a, we call the segment of the line contained within the box an a-segment. Otherwise, we call it a b-segment. We consider the possible feasible combinations of a-segments and b-segments for each pallet dimension independently.
Figure 2 Example of identifying segments in a loaded pallet.
The horizontal line H - H' crosses 4 boxes, two across the a dimension (two a-segments) and two across the b dimension (two b-segments). The vertical line V - V' crosses 5 boxes, one across the a dimension and 4 across the b dimension.
Let (n, m) denote an ordered pair of nonnegative integers satisfying
n * a + m * b
S
for a pallet dimension S, which could be X or Y. Such an
ordered pair (n, m) is called a feasible partition of S.
If n and m also satisfy 0
S - n
* a - m * b < b, then (n, m) is called an efficient
partition of S [Bischoff and Dowsland 1982].
Dowsland [1984] shows that if two instances of PLP possess the same set of efficient partitions for both the pallet width and length, then both instances share the same set of optimal solutions. This defines a relation in the set of instances of PLP, which is reflexive, symmetric, and transitive. Therefore, the set of instances of PLP can be divided into equivalence classes, based on the set of efficient partitions. If a solution is known for a class representative, then this solution can be used on any other instance in the class. Because multiplying all dimensions by an integer produces a new instance in the same class, it is easy to see that each class contains infinitely many instances.
If, in addition, n and m satisfy n * a + m * b = S, then (n, m) is called a perfect partition of S [Dowsland 1984]. In general, the sets of perfect partitions of a given instance can be empty, but the instance of an equivalence class with minimal pallet dimensions contains at least one perfect partition for each dimension, X and Y [Dowsland 1984]. This is easily observed if we consider an arbitrary instance without a perfect partition for a given dimension. In this case, we can reduce the corresponding dimension of the pallet without altering the set of efficient partitions. This implies that the new instance, with a smaller pallet dimension, also belongs to the same class.
The files listed below contain a list of all equivalence classes with a area ratio - the ratio of the area of the pallet by the area of the box - of up to 10, 20, 50 and 100.
Under Construction
